Planificación de microclase
Objetivos:
Objetivo de Aprendizaje / Logros / Competencias / Estándares:
- Los y las estudiantes representaran gráficamente fracciones propias e impropia, a través de figuras geométricas planas en el ordenador.
- los y las estudiantes identificarán y construirán fracciones equivalentes a partir de su representación gráfica y de la aplicación de la propiedad fundamental de las proporciones.
- Los y las estudiantes realizarán suma y resta de fracciones a través de solución de problemas y representación gráfica de fracciones
- Los y las estudiantes realizarán algoritmos de multiplicación y división de fracciones a través del uso de ordenador y programa scratch
- los y las estudiantes transformarán un número mixto en fracción y viceversa a través de procedimientos algorítmicos de suma, resta, multiplicación, y división
Propósito
Duración
1 sección de dos horas cada una.(90 minutos).
Actividad docente
Duración
1 sección de dos horas cada una.(90 minutos).
Actividad docente
- 3.Explicacion concepto de fracción, representación gráfica de fracciones propias e impropias y sus operaciones básicas. (presentación de vídeo)
Definir Actividad 1
En esta sesión el docente va a compartirle a sus estudiantes sobre el proyecto; la importancia y justificación del mismo para que los estudiantes se ubiquen en las actividades a realizar y las condiciones del mismo.
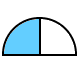
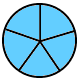
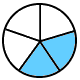
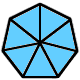
También el docente explicará el concepto de fracción y la representación gráfica de Fracciones propias e impropias.
Primera Sesión
1.Presentación:
2. Diagnóstico inicial.
Requisitos
- Reconocer figuras geométricas planas básicas.
- Uso básico programa scratch.
- Uso básico de Hoja de calculo.
- Uso básico procesador de texto microsoft word
- Orden y disciplina.
Herramientas
Procesador de TextoInternet - InformaciónHoja de CálculoAlgoritmos y programaciónScratchFracción Propia | |
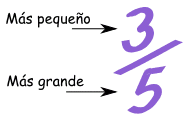 | Una fracción propia es una fracción donde el numerador (el número de arriba) es menor que el denominador (el número de abajo). Ejemplo: 1/4 (un cuarto) y 5/6 (cinco sextos) son fracciones propias. |
Fracción Impropia | |
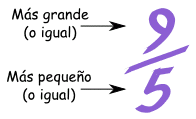 | Una Fracción Impropia es una fracción en donde el numerador (el número de arriba) es mayor o igual que el denominador (el número de abajo). Ejemplo: 5/3 (cinco tercios) y 9/8 (nueve octavos) son fracciones impropias. Las fracciones impropias NO son malas. |
Hay tres tipos de fracciones:
| Fracciones propias: | El numerador es menor que el denominador |
|---|---|
| Ejemplos: 1/3, 3/4, 2/7 | |
| Fracciones impropias: | El numerador es mayor (o igual) que el denominador |
| Ejemplos: 4/3, 11/4, 7/7 | |
| Fracciones mixtas: | Un número entero y una fracción propia juntos |
| Ejemplos: 1 1/3, 2 1/4, 16 2/5 |
Fracciones mixtas
Entonces, una fracción mixta es simplemente un númeo entero y una fracción combinadas en un número "mixto".
 Repasemos los tipos de fracciones que conoces...Fracciones propias: son aquellas en las que el numerador es menor que el denominador, por lo tanto, son menores que la unidad. En la recta numérica se ubican entre el 0 y el 1.Fracciones aparentes: son aquellas en las que el numerador es igual al denominador, por lo tanto, son iguales a la unidad.
Repasemos los tipos de fracciones que conoces...Fracciones propias: son aquellas en las que el numerador es menor que el denominador, por lo tanto, son menores que la unidad. En la recta numérica se ubican entre el 0 y el 1.Fracciones aparentes: son aquellas en las que el numerador es igual al denominador, por lo tanto, son iguales a la unidad.  Fracciones decimales: son aquellas en las que el denominador es 10, 100, 1.000, etc., o sea la unidad seguida de ceros.
Fracciones decimales: son aquellas en las que el denominador es 10, 100, 1.000, etc., o sea la unidad seguida de ceros.El Numerador indica el número de partes iguales que se han tomado o considerado de una totalidad. El Denominador indica el número de partes iguales en que se ha dividido una totalidad.
Por ejemplo, la fracción 1 / 6 (se lee: un sexto) tiene como numerador al 1 y como denominador al 6. El 1 significa que se ha considerado 1 parte de un total de 6 partes en que se dividió el entero o el todo.


Fracciones impropias: son aquellas en las que el numerador es mayor que el denominador, por lo tanto, son mayores que la unidad.

Ejemplo
| ||
Problema
|
Escribe
| |
4 • 4 = 16
16 + 3 = 19
|
Multiplica el denominador de la fracción por el número entero.
Suma éste resultado al numerador de la fracción.
El resultado se convierte en el numerador de la fracción impropia.
Nota que el denominador de la fracción impropia es el mismo que el denominador que estaba en la parte fraccional del número mixto.
| |
Respuesta
| ||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
|
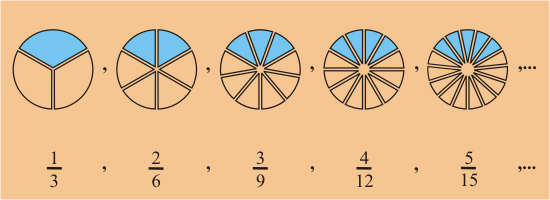
Evaluación
| CATEGORÍA | 4 | 3 | 2 | 1 |
| Razonamiento Matemático | Usa razonamiento matemático complejo y refinado. | Usa razonamiento matemático efectivo. | Alguna evidencia de razonamiento matemático. | Poca evidencia de razonamiento matemático. |
| Estrategia/Procedimientos | Por lo general, usa una estrategia eficiente y efectiva para resolver problemas. | Por lo general, usa una estrategia efectiva para resolver problemas. | Algunas veces usa una estrategia efectiva para resolver problemas, pero no lo hace consistentemente. | Raramente usa una estrategia efectiva para resolver problemas. |
| Terminología Matemática y Notación | La terminología y notación correctas fueron siempre usadas haciendo fácil de entender lo que fue hecho. | La terminología y notación correctas fueron, por lo general, usadas haciendo fácil de entender lo que fue hecho. | La terminología y notación correctas fueron usadas, pero algunas veces no es fácil entender lo que fue hecho. | Hay poco uso o mucho uso inapropiado de la terminología y la notación. |
| Contribución Individual a la Actividad | El estudiante fue un participante activo, escuchando las sugerencias de sus compañeros y trabajando cooperativamente durante toda la lección. | El estudiante fue un participante activo, pero tuvo dificultad al escuchar las sugerencias de los otros compañeros y al trabajar cooperativamente durante la lección. | El estudiante trabaja con su(s) compañero(s), pero necesito motivación para mantenerse activo. | El estudiante no pudo trabajar efectivamente con su compañero/a. |
| Explicación | La explicación es detallada y clara. | La explicación es clara. | La explicación es un poco difícil de entender, pero incluye componentes gráficos. | La explicación es difícil de entender y tiene varios componentes ausentes o no fue incluida. |
| Orden y Organización | El trabajo es presentado de una manera ordenada, clara y organizada que es fácil de leer. | El trabajo es presentado de una manera ordenada y organizada que es, por lo general, fácil de leer. | El trabajo es presentado en una manera organizada, pero puede ser difícil de leer. | El trabajo se ve descuidado y desorganizado. Es difícil saber que información está relacionada. |
| Conceptos Matemáticos | La explicación demuestra completo entendimiento del concepto matemático usado para resolver los problemas. | La explicación demuestra entendimiento sustancial del concepto matemático usado para resolver los problemas. | La explicación demuestra algún entendimiento del concepto matemático necesario para resolver los problemas. | La explicación demuestra un entendimiento muy limitado de los conceptos subyacentes necesarios para resolver problemas o no está escrita. |
| Diagramas y Dibujos | Los diagramas y/o dibujos son claros y ayudan al entendimiento de los procedimientos. | Los diagramas y/o dibujos son claros y fáciles de entender. | Los diagramas y/o dibujos son algo difíciles de entender. | Los diagramas y/o dibujos son difíciles de entender o no son usados. |
















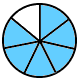


buen explicdo
ResponderEliminar